Statistischer Rang

Angelegt Donnerstag 05 Dezember 2024

Im Folgenden habe ich den Rang (engl. "rank") zu einer Stichprobe s() als MMBASIC Subroutine programmiert. Die Datei heißt "rank.inc" weil ich sie auf einem Colour Maximite 2 (CMM2) als "#include" Modul verwende.
Das ist ein Import Mechanismus wie man ihn von Modula-2, C oder Python kennt - man lädt externen Code hinzu, wenn man die entsprechende Funktion oder Routine benötigt.

Wie die "Rang-Zahlen" berechnet werden, wird in diesem PDF (http://statistikpaket.mathe-total.de/Manual/Berechnung-von-Rangzahlen.pdf) erklärt.

Um die Prozedur rank s(), r() sinnvoll nutzen zu können, muss das importierende Programm eine Stichprobe s(n) mit n Werten und ein leeres Feld r(n) in gleicher Größe übergeben.
Nach dem Aufruf rang s(),r() befinden sich in r() die Rangzahlen der Stichprobe s(). Die Größe der Stichprobe ist nur durch den verfügbaren Speicher begrenzt.
Auf einem Raspberry Pi Pico2W lassen sich 4000 normalverteilte Zufallszahlen in ca. 2 Sekunden ranken. Der CMM2 braucht 1.76 Sekunden für die gleiche Aufgabe.
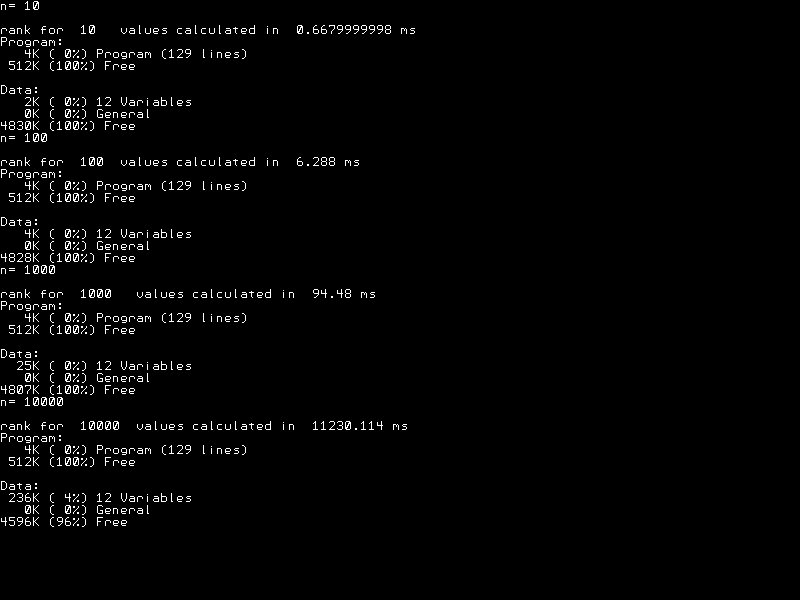
Versuche zeigen, dass die Zeitkomplexität des Algorithmus zwischen O(n) und O(n²) liegt.

Der Übergang von 10 -> 100 ist O(n), der von 100 -> 1000 könnte noch O(n) sein, der von 1000 -> 10000 sieht eher nach O(n²) aus.
Die Zeitkomplexität scheint mit größerem Stichprobenumfang n gegen O(n²) anzusteigen. Vermutlich gibt es dann mehr "gleiche" Werte in s(), welche eine die Berechnung des mittleren Ranges und dessen Einsetzen in das Ergebnis erfordern ("Case Else").
Da dieser "Case Else" Fall seinerseits eine Schleife enthält nähert sich hier O(n) dem O(n²).

_{quadratischer Aufwand}
Der eher quadratische zeitliche Aufwand O(n²) zeigt sich deutlich, wenn man n=10000 und n=20000 gegenüberstellt.

_{Bei doppeltem n ergibt sich 4-facher Zeitauwand und doppelter Speicherbedarf.}

Anwendungsbeispiel:

#include "rank.inc"
dim s(4) = (0,-1.1,2,-1.1)
dim r(4)
rank s(),r()
. . .
Eine Ausgabe, welche i, s(i) und r(i) auflistet, würde folgendes Ergebnis zeigen:


			i 	      s(i)		 r(i)
			1		0		   3 	0 ist die drittgrößte Zahl
			2	     -1.1		 1.5    -1.1 nimmt Platz 1 und Platz 2 im Ranking ein, daher ist der Rang = (1+2)/2
			3		2		   4	2 ist die größte Zahl auf dem letzten Platz 4 im Ranking
			4	     -1.1		 1.5	-1.1 teilt sich Platz 1 und Platz 2 mit der Zahl in Zeile 2 und hat daher den Rang (1+2)/2

' rank.inc - Version 1.8
' given the test sample s(n) with 'n' values, calculate the rank r(n) of 'n' ranking values
' (c) Andreas Mueller, 2024

Option base 1

'-------- helping functions and subroutines -----------------

Function sum(a%,b%) As Integer ' sum of integers from a% to b%
if b% < a% Then

Print "error b% < a% in function sum(a%,b%)"
End

Else

sum = (b%-a%+1)*(a%+b%)/2

End if
End Function

Sub valuesUnique in(),out()
Local size
Local i=1
size = Bound(in())
Do

If i = 1 Then

out(i)=1

Else

If in(i)=in(i-1) Then

out(i)=out(i-1)+1
out(i-1)=0

Else

out(i)=1

End If

End If
Inc i

Loop Until i>size
End Sub

Sub calculateRank b%(),e(),r()
Local size
Local i=1
Local ri
Local k
size = Bound(b%())
Do

Select Case e(i)

Case 0

' do nothing

Case 1

r(b%(i)) = i

Case Else

ri = sum(i-e(i)+1,i)/e(i)
For k = i-e(i)+1 To i

r(b%(k)) = ri

Next k

End Select
Inc i

Loop Until i>size
End Sub

'------------------------------------------------------------
Sub rank s(),r() ' calculate rank r() from statistic s()
'------------------------------------------------------------
Local n = Bound(s())
Local b%(n)
Local e(n)

Sort s(),b%() ' after the sort b%() will contain the original index position of each element in s() being sorted
valuesUnique s(),e()
calculateRank b%(),e(),r()

Local i
Local su=0
For i = 1 To n

su = su + r(i)

Next i
If su = n*(n+1)/2 Then

' ok

Else

Print "Error Sub rank s(),r()"
End

End If
End Sub

_{Berechnung des Rang von 10 normalverteilten Zufallszahlen mit Anzeige in der Hilfsindizes zum besseren Verständnis des Algorithmus. o()=s()}